sử dụng Sơ Đồ Tư Duy Hình Học 12 Chương 1, Sơ Đồ Tư Duy Toán Lớp 12 Cực Chất-SONGIA

Sau khi đã nấu xong gần như bài học của chương Khối đa diện, chúng ta đơn sơ nhận thấy để học tốt chương này thì việc nắm vững kiến thức hình học không gian ở lớp 11 là yếu tố mang tính chất quyết định đến khả năng tiếp thu bài và giải bài tập. Bài ôn tập chương Khối đa diện sẽ khối hệ thống lại tất cả kiến thức cần nắm thông qua những sơ đồ tư duy, hy vọng sẽ sẽ cho cho gần như em có định hướng học tập hiệu suất cao hơn.

Đang xem : Sơ đồ tư duy hình học 12 chương 1

1. Video ôn tập chương 1

2. Tóm tắt lý thuyết

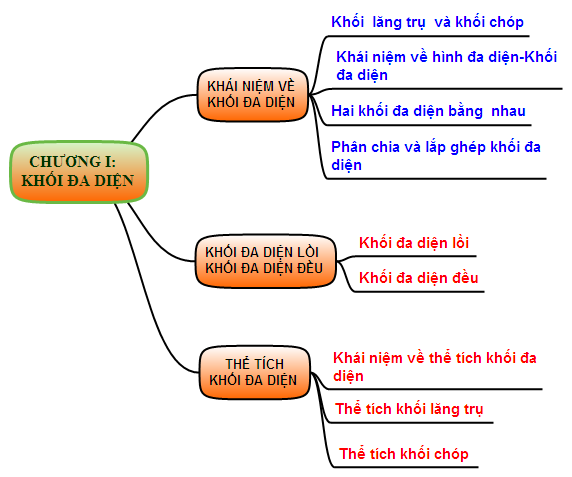
2.1. Sơ đồ nội dung chương khối đa diện
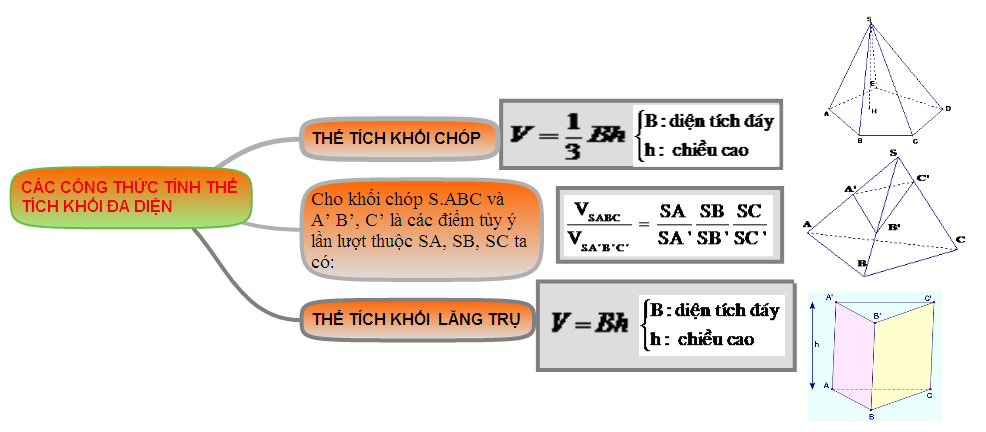
2.2. Sơ đồ gần như công thức tính thể tích khối đa diện
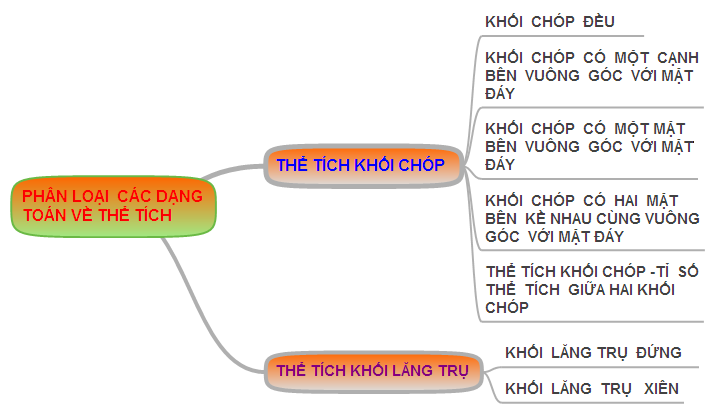
2.3. Sơ đồ phân loại gần như dạng toán về thể tích
2.4. khối hệ thống hóa kỹ năng và kiến thức hình học khoảng trống lớp 11

3. Bài tập minh hoạ

4. Luyện tập ôn tập Chuơng 1 Toán 12

4.1 Trắc nghiệm ôn tập hình học 12 chương 1
4.2 Bài tập SGK và Nâng Cao khối đa diện

5. Hỏi đáp về khối đa diện

a ) Quan hệ song song

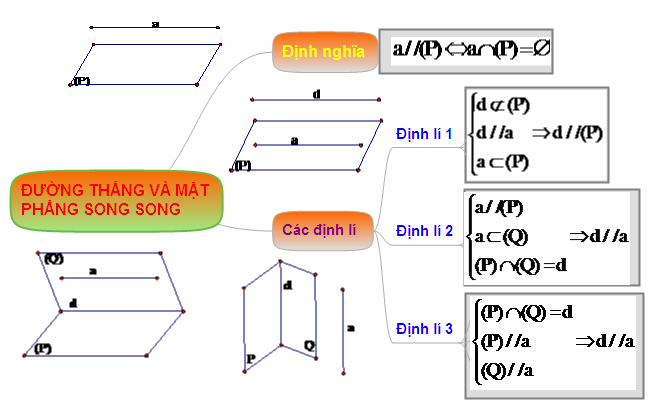
khối hệ thống hóa kiến thức “Đường thẳng và mặt phẳng song song”

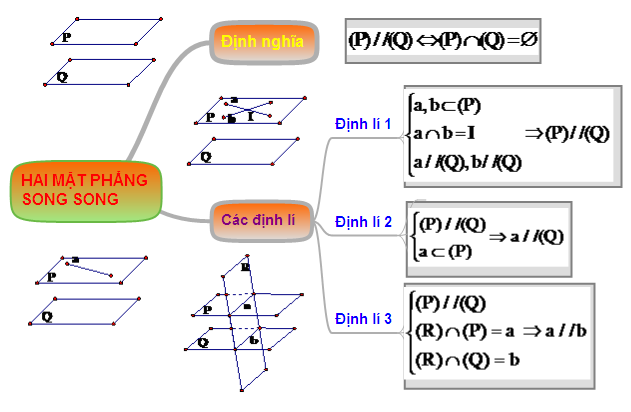
khối hệ thống hóa kiến thức “Hai mặt phẳng song song”

b ) Quan hệ vuông góc

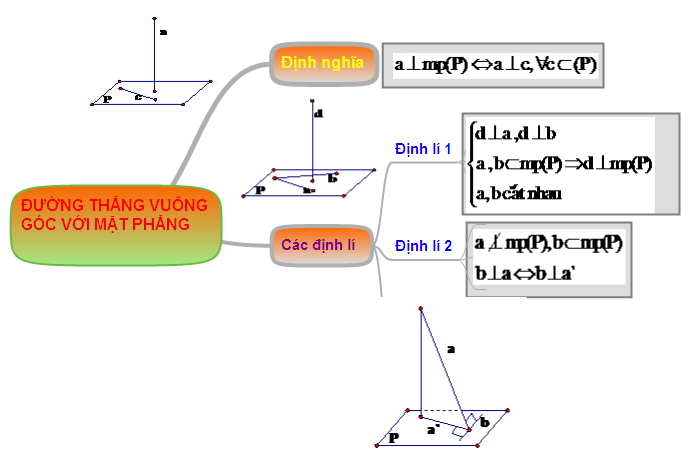
khối hệ thống hóa kiến thức “Đường thẳng vuông góc với mặt phẳng”

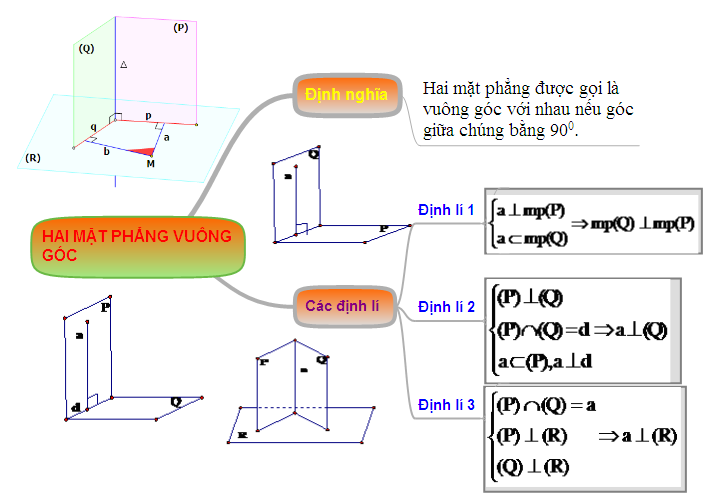
khối hệ thống hóa kiến thức “Hai mặt phẳng vuông góc”

c ) khoảng cách và góc

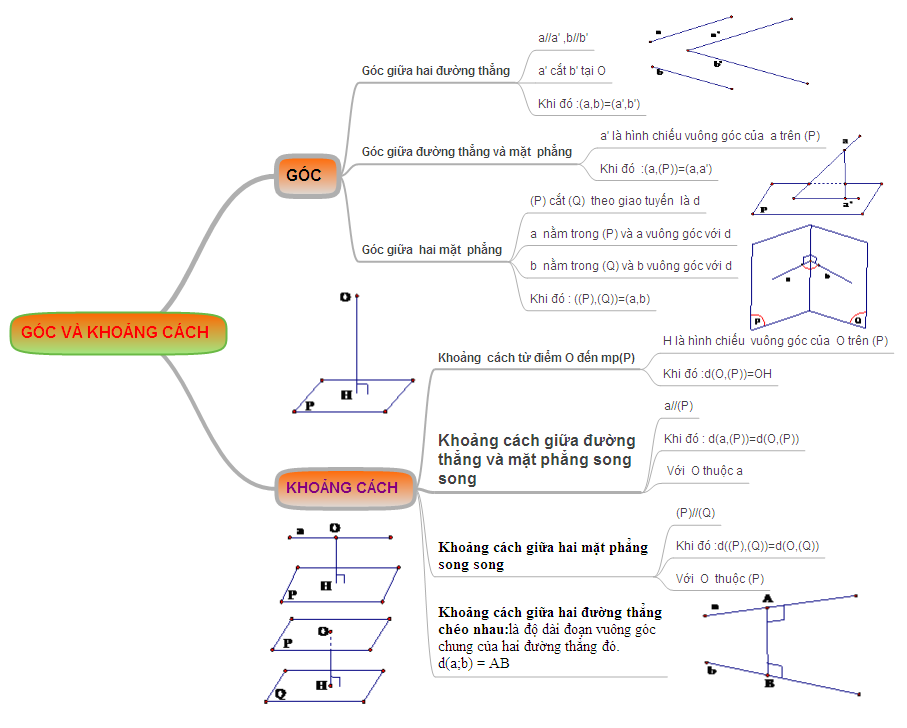
khối hệ thống hóa kiến thức “khoảng cách và góc”

Bài tập 1:

Cho hình lăng trụ ABC.A ” B ” C ” có đáy ABC là tam giác đều cạnh ( 2 asqrt2 ) và ( AA ” = asqrt3 ). Hình chiếu vuông góc của điểm A ” trên mặt phẳng ( ABC ) trùng với trọng tâm G của tam giác ABC. Tính theo a thể tích khối lăng trụ ABC.A ” B ” C ” và khoảng cách từ điểm C đến mặt phẳng ABB ” A ” .

Lời giải:

Tính ( V_ABC. A ” B ” C ” ) .

Ta có(A”G ot left( ABC
ight) Rightarrow A”G)là chiều cao của lăng trụ ABC.A”B”C”.

Diện tích tam giác đều ABC là : ( S_ABC = AB ^ 2.fracsqrt 3 4 = 2 a ^ 2 sqrt 3 ) .
Gọi M là trung điểm của BC, ta có : ( AM = BC.fracsqrt 3 2 = 2 asqrt 2. fracsqrt 3 2 = asqrt 6 ) .
( AG = frac23AM = frac2asqrt 6 3 ) .

Trong(Delta A”GA) vuông tại G, ta có(A”G = sqrt A”A^2 – AG^2 = sqrt 3a^2 – frac83a^2 = fracasqrt 3 3).

Vậy thể tích khối lăng trụ ABC.A ” B ” C ” là :
( V_ABC. A ” B ” C ” = S_ABC. A ” G = 2 a ^ 3 )

Tính(dleft( C,left( ABB”A”
ight)
ight))

Gọi N là trung điểm của AB .
Trong ( Delta A ” GN ), kẻ ( GH ot A ” N ) .
. : Cách Chuyển Nhạc Từ Nhaccuatui Sang Zing Mp3 Trên Iphone Đơn Giản, Nhanh Nhất

Chứng minh được(GH ot left( ABB”A”
ight))tại H.

Suy ra(dleft( G,left( ABB”A”
ight)
ight) = GH).

Ta có ( CN = AM = asqrt 6 ), ( GN = frac13CN = fracasqrt 6 3 ) .
( frac1GH ^ 2 = frac1A ” G ^ 2 + frac1GN ^ 2 = frac3a ^ 2 + frac96a ^ 2 = frac92a ^ 2 ) ( Rightarrow GH = fracasqrt 2 3 ) .

Do đó(dleft( G,left( ABB”A”
ight)
ight) = GH = fracasqrt 2 3).

Vậy(dleft( C,left( ABB”A”
ight)
ight) = 3dleft( G,left( ABB”A”
ight)
ight) = asqrt 2).

Bài tập 2:

Cho hình chóp S.ABC, tam giác ABC vuông tại B, ( AB = a, widehat ACB = 60 ^ 0, SAperp ( ABC ) ). Tính thể tích khối chóp S.ABC theo a và cosin của góc giữa hai mặt phẳng ( SAC ) và ( SBC ), biết khoảng cách từ điểm A đến mặt phẳng ( SBC ) bằng ( fraca2 ) .

Lời giải:

Tính thể tích khối chóp S.ABC :

(eginarrayl left{ eginarrayl SA ot (ABC) Rightarrow BC ot SA BC ot AB endarray
ight. Rightarrow BC ot (SAB) Rightarrow (SBC) ot (SAB). endarray)

Kẻ AH vuông góc SB ( ( H in SB ) ) suy ra : ( AH ot ( SBC ) Rightarrow AH = fraca2. ) ( BC = fracAB an 60 ^ 0 = fracasqrt 3 3. )
( frac1AH ^ 2 = frac1AB ^ 2 + frac1SA ^ 2 Rightarrow SA = fracasqrt 3 3. )
Diện tích tam giác ABC là : ( S_Delta ABC = fraca ^ 2 sqrt36 ) .
Vậy thể tích khối chóp là : ( V_S. ABC = fraca ^ 318. )
Tính cosin của góc giữa hai mặt phẳng ( SAC ) và ( SBC )
Kẻ ( BI ot AC ;, , IK ot SC. )

Ta có:(left{ eginarrayl BI ot AC BI ot SA endarray
ight. Rightarrow BI ot (SAC) Rightarrow SC ot BI)(1)

Mặt khác : ( IK ot SC ) ( 2 )
( SC ot ( BIK ) Rightarrow BK ot SC. ) Suy ra góc giữa 2 mặt phẳng là ( widehatIKB ). Xét gần như tam giác vuông ABC và SBC ta tính được độ nhiều năm gần như đường cao : ( BI = fraca2 ; BK = frac2asqrt1515 ). Xét tam giác BIK vuông tại I ta có : ( IK = fracasqrt1530 ; coswidehatIKB = frac14 ) .
. : Xem Phim Bạn Trai Tôi Là Hồ Ly Tập 1, Vietsub + Thuyết Minh Full Hd

Bài tập 3:

Cho hình chóp S.ABCD có thể tích bằng 48 và ABCD là hình thoi. gần như điểm M, N, P., Q. lần lượt là gần như điểm trên gần như đoạn SA, SB, SC, SD thỏa mãn nhu cầu : ( SA = 2SM, SB = 3SN ; ) ( SC = 4SP ; SD = 5SQ. ) Tính thể tích V của khối chóp S.MNPQ.

Lời giải:

Ta có : ( V_SMNPQ = V_SMQP + V_SMNP )
Và : ( V_SADC = V_SQBC = frac12V_S. ABCD )
Mặt khác :

(eginarrayl fracV_S.MQPV_S.ADC = fracSQSD.fracSMSA.fracSPSC = frac15.frac12.frac14 = frac140 Rightarrow V_S.MQP = frac140.V_S.ADC = frac180.V_S.ABCD endarray)

( eginarrayl fracV_S. MNPV_S. ABC = fracSMSA. fracSPSC. fracSNSP = frac12. frac14. frac13 = frac124 Rightarrow V_S. MNP = frac124V_S. ABC = frac148. V_S. ABCD endarray )

(Rightarrow V_SMNPQ = left( frac180 + frac148
ight)V_S.ABCD = frac85)

. bài viết thuộc chuyên mục: Tư duy

Post navigation

Source: https://suachuatulanh.edu.vn
Category : Tư Vấn Hỗ Trợ