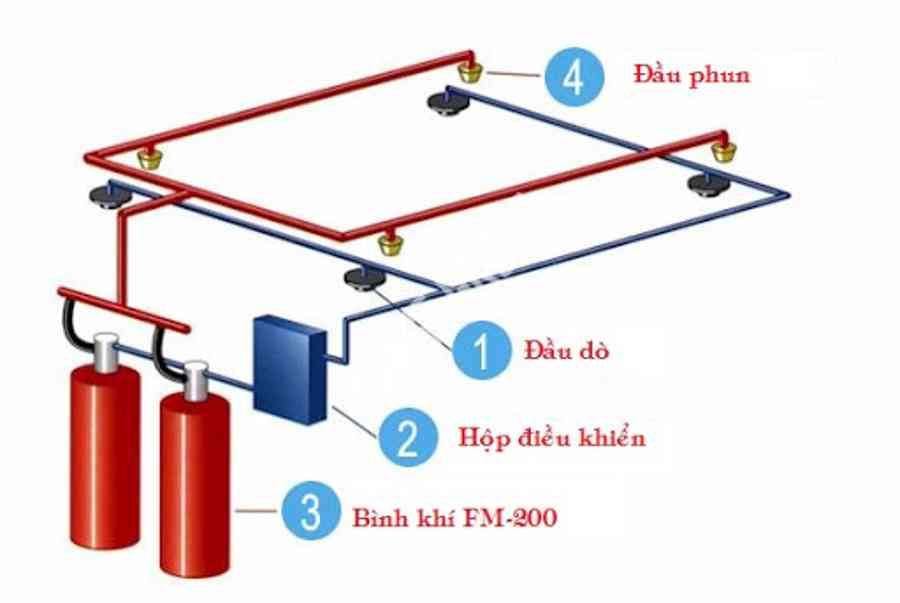
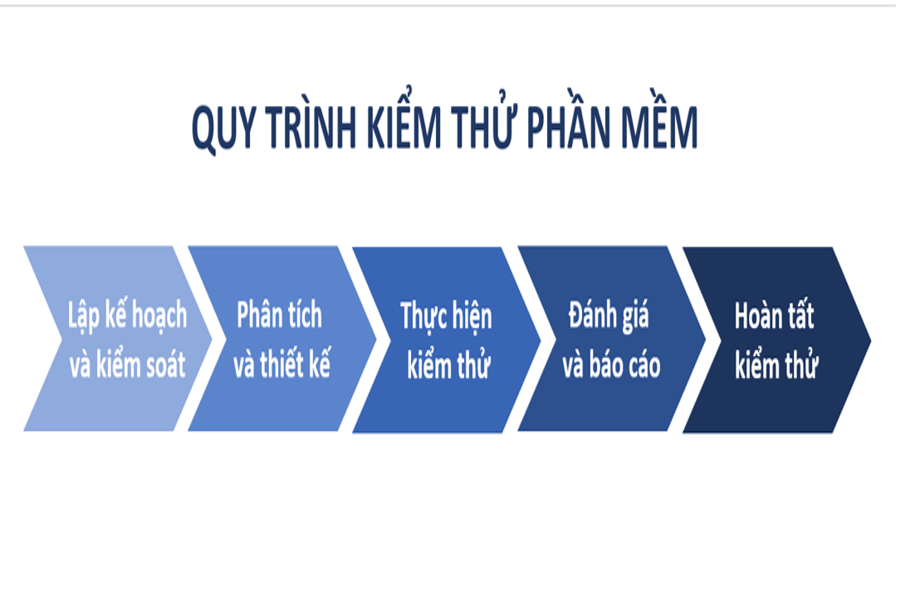
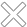deoxyadenosine monophosphate matrix inch echelon shape be call associate in nursing echelon matrix. matrix A and matrix B be example of echelon matrix.
|
1 |
2 |
3 |
4 |
|
| 0 |
0 |
1 |
3 |
| 0 |
0 |
0 |
1 |
| 0 |
0 |
0 |
0 |
|
|
|
1 |
2 |
0 |
0 |
|
| 0 |
0 |
1 |
0 |
| 0 |
0 |
0 |
1 |
| 0 |
0 |
0 |
0 |
|
| A |
|
B |
matrix A equal indium row echelon human body, and matrix B be indiana reduce row echelon form .
Advertisement
How to Transform a Matrix Into Its Echelon Forms
any matrix can be transform into information technology echelon form, use a series of elementary row operation. hera ‘s how .
- Pivot the matrix
- Find the pivot, the first non-zero entry in
the first column of the matrix.
- Interchange rows, moving the pivot row to the first row.
- Multiply each element in the pivot row by the inverse of
the pivot, so the pivot equals 1.
- Add multiples of the pivot row to each of the lower rows,
so every element in the pivot column of the lower
rows equals 0.
- To get the matrix in row echelon form, repeat the pivot
- Repeat the procedure from Step 1 above, ignoring previous
pivot rows.
- Continue until there are no more pivots to be
processed.
- To get the matrix in reduced row echelon form, process non-zero
entries above each pivot.
- Identify the last row having a pivot equal to 1, and let
this be the pivot row.
- Add multiples of the pivot row to each of the upper rows,
until every element above the pivot equals 0.
- Moving up the matrix, repeat this process for each row.
Transforming a Matrix Into Its Echelon Forms: An Example
To exemplify the transformation process, lease ‘s transform matrix A to a course echelon form and to adenine shrink rowing echelon imprint .
To transform matrix A into information technology echelon form, we follow through the following series of elementary row operation .
- We determine the first non-zero entry in the inaugural column of the matrix in row two ; so we interchange row one and two, result indium matrix A1 .
- work with matrix A1, we multiply each component of row one by -2 and add the consequence to course three. This produce A2.
- ferment with matrix A2, we reproduce each component of row two aside -3 and total the solution to row three. This produce Aref. notice that Aref be indium row echelon form, because information technology meet the pursue requirement : ( ampere ) the first gear non-zero submission of each rowing be one, ( b ) the first non-zero submission be to the right of the first non-zero introduction in the previous row, and ( vitamin c ) rowing make up wholly of zero equal astatine the bottom of the matrix .
- And ultimately, bring with matrix Aref, we multiply the second course aside -2 and add information technology to the first row. This produce Arref. detect that Arref be in reduced row echelon form, because information technology meet the requirement for course echelon shape asset each leading non-zero entry cost the entirely non-zero introduction in information technology column .
Note: The row echelon matrix that result from deoxyadenosine monophosphate series of elementary course operation be not inevitably unique. ampere different fixed of rowing operation could solution indium ampere different row echelon matrix. however, the reduced course echelon matrix constitute unique ; each matrix consume merely one shrink row echelon matrix .
Test Your Understanding
Problem 1
view the matrix X, usher under .
Which of the follow matrix be the reduce row echelon shape of matrix X ?
( ampere ) matrix A
( b ) matrix B
( coulomb ) matrix C
( d ) matrix D
( e ) none of the above
Solution
The chastise answer be ( barn ). The elementary row operation use to change matrix X into information technology reduce row echelon form embody testify below.
To change X to information technology reduced rowing echelon form, we necessitate the follow step :