Nguyên tử hydro – Wikipedia tiếng Việt

03/04/2023 admin
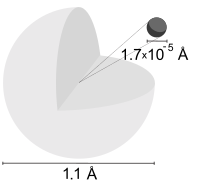Mô phỏng một nguyên tử hydro cho thấy đường kính bằng xấp xỉ hai lần bán kính mô hình Bohr. (Ảnh mang tính minh họa)

Một nguyên tử hydro là một nguyên tử của nguyên tố hóa học hydro. Nguyên tử điện tích trung lập, chỉ chứa duy nhất một hạt proton mang điện tích dương và một hạt electron mang điện tích âm, bị ràng buộc với hạt nhân bởi lực Coulomb. Nguyên tử hydro cấu thành khoảng 75% khối lượng baryon của vũ trụ.[1]

Trên Trái Đất, những nguyên tử hydro bị cô lập là rất hiếm. Thay vào đó, hydro có khuynh hướng phối hợp với những nguyên tử trong xuất hiện trong những hợp chất, hoặc với chính nó để tạo thành khí hydro, H2 .Việc tăng trưởng một triết lý để hiểu rõ đặc thù của nguyên tử hydro khá quan trọng trong lịch sử dân tộc cơ học lượng tử .

Đồng vị giàu nhất, hydro-1, proti, hay còn gọi là hydro nhẹ, không chứa bất kì hạt neutron nào và chỉ đơn giản là một proton và một electron. Proti là ổn định và cấu thành nên 99.9885% các nguyên tử hydro trong tự nhiên.

Deuteri, có hạt nhân chứa một neutron và một proton. Nguyên tử này không thay đổi và cấu thành nên 0.0115 % hydro tự nhiên, được sử dụng trong công nghiệp cho lò phản ứng hạt nhân và cộng hưởng từ hạt nhân .Triti chứa hai neutron và một proton, không không thay đổi, phân rã với một chu kì bán rã 12,32 năm. Vì bán rã nên triti không sống sót trong tự nhiên, ngoại trừ trong những lượng vết .Các đồng vị cao hơn của hydro chỉ được tạo ra một cách tự tạo bằng những máy gia tốc hạt và những lò phản ứng, và chúng bán rã trong vòng 10 − 22 giây .Các công thức ở dưới đều đúng cho tổng thể ba đồng vị của hydro, nhưng phải sử dụng những giá trị hơi khác nhau của hằng số Rydberg ( sửa đúng công thức được đưa ra bên dưới ) cho mỗi loại đồng vị hydro .
Hydro tìm thấy trong điều kiện kèm theo thông thường ( nhiệt độ và áp suất phòng ) luôn luôn đi kèm theo với electron của nó, do ion hydro rất dễ bị phản ứng. Khi ion hydro viết là ” H + ” như trong sự sonvat hóa của những axit như axit clohydric, hydroni, H 3 O +, có nghĩa là, không phải là một nguyên tử hydro đơn lẻ bị ion hóa. Trong trường hợp đó, acid chuyển proton vào H2O để tạo thành H3O + .Ion hydro không có electron, hoặc những proton tự do có phổ cập trong môi trường tự nhiên liên sao, và trong gió mặt trời .

Phân tích giả định[sửa|sửa mã nguồn]

Nguyên tử hydro có ý nghĩa đặc biệt quan trọng trong cơ học lượng tử và kim chỉ nan trường lượng tử như một mạng lưới hệ thống vật lí yếu tố hai vật đơn thuần, đã mang lại nhiều chiêu thức giải biểu thức dạng đóng .

Mô phỏng cổ xưa thất bại[sửa|sửa mã nguồn]

Thí nghiệm của Ernest Rutherford năm 1909 cho thấy cấu trúc của nguyên tử là một khối đặc, hạt nhân điện dương với một hạt điện âm nhẹ quay xung quanh nó. Việc này ngay lập tức gây ra yếu tố về việc làm thế nào mà một mạng lưới hệ thống như vậy hoàn toàn có thể không thay đổi. Điện từ học cổ xưa đã chỉ ra rằng bất kể tần suất phát ra nguồn năng lượng nào sẽ được mô phỏng trải qua công thức Larmor. Nếu hạt electron mà nằm trong một quỹ đạo tròn tuyệt vời và hoàn hảo nhất và phát ra nguồn năng lượng liên tục, nó sẽ nhanh gọn rơi xoắn ốc vào trong hạt nhân với một thời hạn rơi khoảng chừng :

t fall ≈ a 0 3 4 r 0 2 c ≈ 1.6 ⋅ 10 − 11 s { \ displaystyle t_ { \ text { fall } } \ approx { \ frac { a_ { 0 } ^ { 3 } } { 4 r_ { 0 } ^ { 2 } c } } \ approx 1.6 \ cdot 10 ^ { – 11 } { \ text { s } } }{\displaystyle t_{\text{fall}}\approx {\frac {a_{0}^{3}}{4r_{0}^{2}c}}\approx 1.6\cdot 10^{-11}{\text{s}}}

a

0

{\displaystyle a_{0}}

{\displaystyle a_{0}} là bán kính Bohr và

r

0

{\displaystyle r_{0}}

{\displaystyle r_{0}} là bán kính điện từ cổ điển. Nếu điều này là đúng, tất cả các nguyên tử ngay lập tức sẽ sụp đổ, tuy nhiên các nguyên tử dường như lại ổn định. Hơn nữa, việc rơi xoắn ốc vào bên trong sẽ phát hành ra một tần số điện từ khi quỹ đạo đã nhỏ hơn. Thay vào đó, các nguyên tử được quan sát chỉ phát ra các tần số bức xạ rời rạc. Cách giải quyết sẽ nằm trong việc phát triển của cơ học lượng tử.

Vào năm 1913, Niels Bohr đo được những mức nguồn năng lượng và tần số quang phổ của nguyên tử hydro sau khi làm một số ít giả định đơn thuần để cố gắng nỗ lực thay thế sửa chữa quy mô cổ xưa đã bị thất bại. Giả định gồm có :

  1. Electron chỉ có thể tồn tại trong quỹ đạo tròn nhất định, riêng lẻ hay trạng thái tĩnh tại, do đó có những bán kính và năng lượng riêng lẻ nhất định.
  2. Electron không phát ra phóng xạ khi ở một trong những trạng thái này.
  3. Một electron có thể đạt được hay mất đi năng lượng bằng cách nhảy từ một quỹ đạo riêng lẻ sang một quỹ đạo khác.

Bohr cho rằng mô men động lượng của electron được lượng tử hóa với những giá trị :

L
=
n
ℏ

{\displaystyle L=n\hbar }

{\displaystyle L=n\hbar } với 

n
=
1
,
2
,
3
,
.
.
.

{\displaystyle n=1,2,3,…}

{\displaystyle n=1,2,3,...}

với

ℏ

{\displaystyle \hbar }

{\displaystyle \hbar } là hằng số Plank trên 

2
π

{\displaystyle 2\pi }

{\displaystyle 2\pi }. Ông ấy cũng nghĩ rằng, lực hướng tâm giữ electron nằm trong quỹ đạo của mình, được phân phát bởi lực Coulomb, và năng lượng đó được bảo tồn. Bohr suy ra được năng lượng của mỗi quỹ đạo của nguyên tử hydro là:[2]

E n = − m e e 4 2 ( 4 π ϵ 0 ) 2 ℏ 2 1 n 2 { \ displaystyle E_ { n } = – { \ frac { m_ { e } e ^ { 4 } } { 2 ( 4 \ pi \ epsilon _ { 0 } ) ^ { 2 } \ hbar ^ { 2 } } } { \ frac { 1 } { n ^ { 2 } } } }{\displaystyle E_{n}=-{\frac {m_{e}e^{4}}{2(4\pi \epsilon _{0})^{2}\hbar ^{2}}}{\frac {1}{n^{2}}}}

với

m

e

{\displaystyle m_{e}}

{\displaystyle m_{e}} là khối lượng nghỉ electron,

e

{\displaystyle e}

{\displaystyle e} là điện tích cơ bản,

ϵ

0

{\displaystyle \epsilon _{0}}

\epsilon _{0} là độ từ thấm, và

n

{\displaystyle n}

n là số lượng tử (bây giờ được biết đến như là số lượng tử chính). Dự đoán của Bohr phù hợp với những thí nghiệm đo chuỗi quang phổ của Hydro trước đó, tạo thêm cơ sở vững chắc về một lí thuyết sử dụng các giá trị lượng tử.

Cho

n
=
1

{\displaystyle n=1}

{\displaystyle n=1}, giá trị

m e e 4 2 ( 4 π ϵ 0 ) 2 ℏ 2 = m e e 4 8 h 2 ε 0 2 = 1 R y = 13.605 692 53 ( 30 ) eV { \ displaystyle { \ frac { m_ { e } e ^ { 4 } } { 2 ( 4 \ pi \ epsilon _ { 0 } ) ^ { 2 } \ hbar ^ { 2 } } } = { \ frac { m_ { \ text { e } } e ^ { 4 } } { 8 h ^ { 2 } \ varepsilon _ { 0 } ^ { 2 } } } = 1R y = 13.605 \ ; 692 \ ; 53 ( 30 ) \, { \ text { eV } } }{\displaystyle {\frac {m_{e}e^{4}}{2(4\pi \epsilon _{0})^{2}\hbar ^{2}}}={\frac {m_{\text{e}}e^{4}}{8h^{2}\varepsilon _{0}^{2}}}=1Ry=13.605\;692\;53(30)\,{\text{eV}}}[3]

được gọi là đơn vị năng lượng Rydberg. Nó có liên quan đến hằng số Rydberg 

R

∞

{\displaystyle R_{\infty }}

{\displaystyle R_{\infty }} của vật lý nguyên tử với 

1

Ry

≡
h
c

R

∞

.

{\displaystyle 1\,{\text{Ry}}\equiv hcR_{\infty }.}

{\displaystyle 1\,{\text{Ry}}\equiv hcR_{\infty }.}

Giá trị chính xác của hằng số Rydberg giả định rằng hạt nhân là lớn vô cùng đối với electron. Với hydro-1, hydro-2 (deuteri), và hydro-3 (triti) hằng số được sửa đổi một chút để sử dụng khối lượng rút gọn của hệ thống, chứ không phải chỉ đơn giản là khối lượng của electron. Tuy nhiên, vì hạt nhân nặng hơn nhiều so với electron nên các giá trị gần như giống nhau. Hằng số Rydberg RM của một nguyên tử hydro (một electron), R được cho là

R

M

=

R

∞

1
+

m

e

/

M

,

{\displaystyle R_{M}={\frac {R_{\infty }}{1+m_{\text{e}}/M}},}

{\displaystyle R_{M}={\frac {R_{\infty }}{1+m_{\text{e}}/M}},}

với

M

{\displaystyle M}

M là khối lượng hạt nhân nguyên tử. Với hydro-1, tỉ lệ 

m

e

/

M
,

{\displaystyle m_{\text{e}}/M,}

{\displaystyle m_{\text{e}}/M,} là khoảng 1/1836 (hay nói cách khác là tỉ lệ khối lượng electron-proton). Với deuteri và triti, tỉ lệ này lần lượt là khoảng 1/3670 và 1/5497. Những con số này, khi cộng thêm 1 vào mẫu số cho sửa chữa rất nhỏ giá trị của R, và do đó chỉ sửa chữa một chút cho tất cả mức năng lượng trong các đồng vị tương ứng của hydro.

Vẫn còn một số ít yếu tố về quy mô của Bohr :

  1. nó thất bại trong việc dự đoán các chi tiết quang phổ khác như là cấu trúc tinh tế và cấu trúc siêu tinh tế
  2. nó chỉ có thể dự đoán mức năng lượng chính xác cho bất kì nguyên tử một electron nào thôi (nguyên tử giống hydro)
  3. những giá trị được dự đoán chỉ chính xác với α 2 ≈ 10 − 5 { \ displaystyle \ alpha ^ { 2 } \ approx 10 ^ { – 5 } }{\displaystyle \alpha ^{2}\approx 10^{-5}}α { \ displaystyle \ alpha }\alpha hằng số cấu trúc tinh tế.

Hầu hết những thiếu sót này được sửa chữa thay thế bởi quy mô sửa đổi từ Bohr của Arnold Sommerfeld. Ông trình làng thêm hai độ tự do, được cho phép một electron chuyển dời trên một quỹ đạo elip ; được bộc lộ bởi độ lệch tâm quỹ đạo và xích vĩ của nó so với một trục được chọn. Điều này tạo ra thêm hai số lượng tử, tương ứng với những mô men động lượng quỹ đạo và hình chiếu của nó lên trục được chọn. Như vậy sẽ sửa lại đúng sự phong phú của những trạng thái ( ngoại trừ cho yếu tố 2 chịu nghĩa vụ và trách nhiệm về spin của electron chưa biết ) được tìm thấy. Hơn nữa, khi vận dụng thuyết tương đối hẹp với những quỹ đạo elip, Sommerfeld đã thành công xuất sắc trong việc suy ra được biểu thức đúng cho cấu trúc tinh xảo của quang phổ hydro ( điều mà giống hệt như trong lí thuyết thuyết Dirac phức tạp nhất ). Tuy nhiên, 1 số ít hiện tượng kỳ lạ được quan sát như hiệu ứng Zeeman không bình thường vẫn bỏ ngỏ, không hề lý giải được. Những yếu tố này đã được xử lý với sự tăng trưởng của cơ học lượng tử và phương trình Dirac. Người ta liên tục nhận xét rằng chính phương trình Schrödinger là hoàn hảo nhất hơn lí thuyết Bohr-Sommerfeld trong việc mô phỏng nguyên tử hydro. Tuy nhiên điều này là không phải đúng, vì hầu hết hiệu quả của việc tiếp cận của cả hai đều trùng lặp hoặc là rất gần giống nhau ( một ngoại lệ đáng chú ý quan tâm là yếu tố của nguyên tử hydro trong từ trường và điện từ trường, không hề xử lý được trong khuôn khổ của lí thuyết Bohr-Sommerfeld ), và cả hai đều thiếu sót do sự vắng mặt của spin electron trong hai lí thuyết. Lí thuyết Bohr-Sommerfeld trọn vẹn thất bại trong việc lý giải những mạng lưới hệ thống nhiều electron ( như nguyên tử heli hoặc phân tử hydro ), chứng tỏ sự thiếu tuyệt vời của nó trong việc miêu tả hiện tượng kỳ lạ lượng tử .

Phương trình Schrödinger[sửa|sửa mã nguồn]

Phương trình Schrödinger bộc lộ sự tăng trưởng của mạng lưới hệ thống lượng tử theo thời hạn, và hoàn toàn có thể phân phối được những câu vấn đáp đúng chuẩn, khá đầy đủ cho nguyên tử hydro phi tương đối .

Cơ học Hamilton của nguyên tử hydro là toán tử động năng và lực hút coulomb giữa proton điện dương và electron điện âm. Bằng cách sử dụng phương trình Schrödinger độc lập thời gian, bỏ qua tất cả các tương tác spin cặp, và sử dụng khối lượng rút gọn 

μ

{\displaystyle \mu }

\mu , phương trình được viết ra:

(

−

ℏ

2

2
μ

∇

2

−

Z

e

2

4
π

ϵ

0

r

)

ψ
(
r
,
θ
,
ϕ
)
=
E
ψ
(
r
,
θ
,
ϕ
)

{\displaystyle \left(-{\frac {\hbar ^{2}}{2\mu }}\nabla ^{2}-{\frac {Ze^{2}}{4\pi \epsilon _{0}r}}\right)\psi (r,\theta ,\phi )=E\psi (r,\theta ,\phi )}

{\displaystyle \left(-{\frac {\hbar ^{2}}{2\mu }}\nabla ^{2}-{\frac {Ze^{2}}{4\pi \epsilon _{0}r}}\right)\psi (r,\theta ,\phi )=E\psi (r,\theta ,\phi )}

Mở rộng toán tử Laplace vào hệ tọa độ cầu :

−

ℏ

2

2
μ

[

1

r

2

∂

∂
r

(

r

2

∂
ψ

∂
r

)

+

1

r

2

sin
⁡
θ

∂

∂
θ

(

sin
⁡
θ

∂
ψ

∂
θ

)

+

1

r

2

sin

2

⁡
θ

∂

2

ψ

∂

ϕ

2

]

−

Z

e

2

4
π

ϵ

0

r

ψ
=
E
ψ

{\displaystyle -{\frac {\hbar ^{2}}{2\mu }}\left[{\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial \psi }{\partial r}}\right)+{\frac {1}{r^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial \psi }{\partial \theta }}\right)+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}\psi }{\partial \phi ^{2}}}\right]-{\frac {Ze^{2}}{4\pi \epsilon _{0}r}}\psi =E\psi }

{\displaystyle -{\frac {\hbar ^{2}}{2\mu }}\left[{\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial \psi }{\partial r}}\right)+{\frac {1}{r^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial \psi }{\partial \theta }}\right)+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}\psi }{\partial \phi ^{2}}}\right]-{\frac {Ze^{2}}{4\pi \epsilon _{0}r}}\psi =E\psi }

Đây là một giá trị riêng phần, phương trình vị phân riêng phần mà hoàn toàn có thể được xử lý trong số lượng giới hạn những hàm đặc biệt. Bằng cách đặt Z = 1 ( cho một proton ), vị trí hàm sóng thông thường, được cho trong hệ tọa độ cầu là :

ψ n ℓ m ( r, ϑ, φ ) = ( 2 n a 0 ) 3 ( n − ℓ − 1 ) ! 2 n ( n + ℓ ) ! e − ρ / 2 ρ ℓ L n − ℓ − 1 2 ℓ + 1 ( ρ ) Y ℓ m ( ϑ, φ ) { \ displaystyle \ psi _ { n \ ell m } ( r, \ vartheta, \ varphi ) = { \ sqrt { { \ left ( { \ frac { 2 } { na_ { 0 } } } \ right ) } ^ { 3 } { \ frac { ( n – \ ell – 1 ) ! } { 2 n ( n + \ ell ) ! } } } } e ^ { – \ rho / 2 } \ rho ^ { \ ell } L_ { n – \ ell – 1 } ^ { 2 \ ell + 1 } ( \ rho ) Y_ { \ ell } ^ { m } ( \ vartheta, \ varphi ) }{\displaystyle \psi _{n\ell m}(r,\vartheta ,\varphi )={\sqrt {{\left({\frac {2}{na_{0}}}\right)}^{3}{\frac {(n-\ell -1)!}{2n(n+\ell )!}}}}e^{-\rho /2}\rho ^{\ell }L_{n-\ell -1}^{2\ell +1}(\rho )Y_{\ell }^{m}(\vartheta ,\varphi )}

Ảnh 3D của ψ 4, 3, 1 { \ displaystyle \ psi _ { 4,3,1 } }{\displaystyle \psi _{4,3,1}}
với :

ρ = 2 r n a 0 { \ displaystyle \ rho = { 2 r \ over { na_ { 0 } } } }{\displaystyle \rho ={2r \over {na_{0}}}}
a 0 { \ displaystyle a_ { 0 } }bán kính Bohr,
L n − ℓ − 1 2 ℓ + 1 ( ρ ) { \ displaystyle L_ { n – \ ell – 1 } ^ { 2 \ ell + 1 } ( \ rho ) }{\displaystyle L_{n-\ell -1}^{2\ell +1}(\rho )}đa thức Laguerre tổng quát của độ

n − ℓ − 1

, và

Y ℓ m ( ϑ, φ ) { \ displaystyle Y_ { \ ell } ^ { m } ( \ vartheta, \ varphi ) \, }{\displaystyle Y_{\ell }^{m}(\vartheta ,\varphi )\,}hàm điều hòa cầu của độ ℓ và hạng m. Lưu ý rằng đa thức Laguerre tổng quát được định những nghĩa khác nhau tùy theo tác giả. Sử dụng ở đây phù hợp với định nghĩa được sử dụng bởi Messiah,[4] và Mathematica.[5] Với những định nghĩa khác, đa thức Laguerre tổng quát kèm theo một yếu tố ( n + ℓ ) ! { \ displaystyle ( n + \ ell ) ! }{\displaystyle (n+\ell )!}[6] hay đa thức Laguerre tổng quát xuất hiện trong hàm sóng hydro lại là L n + ℓ 2 ℓ + 1 ( ρ ) { \ displaystyle L_ { n + \ ell } ^ { 2 \ ell + 1 } ( \ rho ) }{\displaystyle L_{n+\ell }^{2\ell +1}(\rho )}[7]

Các số lượng tử hoàn toàn có thể có giá trị như sau :

n
=
1
,
2
,
3
,
…

{\displaystyle n=1,2,3,\ldots }

{\displaystyle n=1,2,3,\ldots }

ℓ = 0, 1, 2, …, n − 1 { \ displaystyle \ ell = 0,1,2, \ ldots, n-1 }{\displaystyle \ell =0,1,2,\ldots ,n-1}
m = − ℓ, …, ℓ. { \ displaystyle m = – \ ell, \ ldots, \ ell. }{\displaystyle m=-\ell ,\ldots ,\ell .}

Ngoài ra, những hàm sóng được bình thường hóa (tức là tích phân mô đun vuông của chúng bằng 1) và trực giao:

∫ 0 ∞ r 2 d r ∫ 0 π sin ⁡ ϑ d ϑ ∫ 0 2 π d φ ψ n ℓ m ∗ ( r, ϑ, φ ) ψ n ′ ℓ ′ m ′ ( r, ϑ, φ ) = ⟨ n, ℓ, m | n ′, ℓ ′, m ′ ⟩ = δ n n ′ δ ℓ ℓ ′ δ m m ′, { \ displaystyle \ int _ { 0 } ^ { \ infty } r ^ { 2 } dr \ int _ { 0 } ^ { \ pi } \ sin \ vartheta d \ vartheta \ int _ { 0 } ^ { 2 \ pi } d \ varphi \ ; \ psi _ { n \ ell m } ^ { * } ( r, \ vartheta, \ varphi ) \ psi _ { n ‘ \ ell ‘ m ‘ } ( r, \ vartheta, \ varphi ) = \ langle n, \ ell, m | n ‘, \ ell ‘, m ‘ \ rangle = \ delta _ { nn ‘ } \ delta _ { \ ell \ ell ‘ } \ delta _ { mm ‘ }, }{\displaystyle \int _{0}^{\infty }r^{2}dr\int _{0}^{\pi }\sin \vartheta d\vartheta \int _{0}^{2\pi }d\varphi \;\psi _{n\ell m}^{*}(r,\vartheta ,\varphi )\psi _{n'\ell 'm'}(r,\vartheta ,\varphi )=\langle n,\ell ,m|n',\ell ',m'\rangle =\delta _{nn'}\delta _{\ell \ell '}\delta _{mm'},}

với

|

n
,
ℓ
,
m
⟩

{\displaystyle |n,\ell ,m\rangle }

{\displaystyle |n,\ell ,m\rangle } là trạng thái được đại diện bởi hàm sóng

ψ

n
ℓ
m

{\displaystyle \psi _{n\ell m}}

{\displaystyle \psi _{n\ell m}} trong kí hiệu Bra-ket, và

δ

{\displaystyle \delta }

{\displaystyle \delta } là hàm delta Kronecker.[8]

Các hàm sóng trong khoảng trống mô men có tương quan đến những hàm sóng trong khoảng trống vị trí qua một đổi khác Fourier

ϕ ( p, ϑ p, φ p ) = ( 2 π ℏ ) − 3 / 2 ∫ e − i p → ⋅ r → / ℏ ψ ( r, ϑ, φ ) d V, { \ displaystyle \ phi ( p, \ vartheta _ { p }, \ varphi _ { p } ) = ( 2 \ pi \ hbar ) ^ { – 3/2 } \ int e ^ { – i { \ vec { p } } \ cdot { \ vec { r } } / \ hbar } \ psi ( r, \ vartheta, \ varphi ) dV, }{\displaystyle \phi (p,\vartheta _{p},\varphi _{p})=(2\pi \hbar )^{-3/2}\int e^{-i{\vec {p}}\cdot {\vec {r}}/\hbar }\psi (r,\vartheta ,\varphi )dV,}

cho những trạng thái ràng buộc, cho ra tác dụng [ 9 ]

ϕ ( p, ϑ p, φ p ) = 2 π ( n − l − 1 ) ! ( n + l ) ! n 2 2 2 l + 2 l ! n l p l ( n 2 p 2 + 1 ) l + 2 C n − l − 1 l + 1 ( n 2 p 2 − 1 n 2 p 2 + 1 ) Y l m ( ϑ p, φ p ), { \ displaystyle \ phi ( p, \ vartheta _ { p }, \ varphi _ { p } ) = { \ sqrt { { \ frac { 2 } { \ pi } } { \ frac { ( n-l-1 ) ! } { ( n + l ) ! } } } } n ^ { 2 } 2 ^ { 2 l + 2 } l ! { \ frac { n ^ { l } p ^ { l } } { ( n ^ { 2 } p ^ { 2 } + 1 ) ^ { l + 2 } } } C_ { n-l-1 } ^ { l + 1 } \ left ( { \ frac { n ^ { 2 } p ^ { 2 } – 1 } { n ^ { 2 } p ^ { 2 } + 1 } } \ right ) Y_ { l } ^ { m } ( { \ vartheta _ { p }, \ varphi _ { p } } ), }{\displaystyle \phi (p,\vartheta _{p},\varphi _{p})={\sqrt {{\frac {2}{\pi }}{\frac {(n-l-1)!}{(n+l)!}}}}n^{2}2^{2l+2}l!{\frac {n^{l}p^{l}}{(n^{2}p^{2}+1)^{l+2}}}C_{n-l-1}^{l+1}\left({\frac {n^{2}p^{2}-1}{n^{2}p^{2}+1}}\right)Y_{l}^{m}({\vartheta _{p},\varphi _{p}}),}

với | n, ℓ, m ⟩ { \ displaystyle | n, \ ell, m \ rangle } là một đa thức Gegenbauer, và ψ n ℓ m { \ displaystyle \ psi _ { n \ ell m } } nằm trong đơn vị chức năng δ { \ displaystyle \ delta } .Cách giải cho phương trình Schrödinger cho hydro là giải tích phân, tạo một biểu thức đơn thuần cho mức nguồn năng lượng của hydro, và cũng cho những tần số của những vạch quang phổ hydro ; tái tạo lại một cách khá đầy đủ quy mô Bohr, vượt ra ngoài nó. Nó cũng mang lại hai số lượng tử khác, và hình dáng hàm sóng của electron ( ” orbital ” ) cho vô số trạng thái cơ học lượng tử hoàn toàn có thể có, nhờ đó lý giải được những đặc thù bất đẳng hướng của những link nguyên tử .Phương trình Schrödinger cũng vận dụng cho những dạng nguyên tử và phân tử phức tạp hơn. Khi có nhiều hơn một electron hoặc một hạt nhân, cách xử lý là không phải tính tích phân mà cần máy tính hoặc giả định tối giản hóa để triển khai .Vì phương trình Schrödinger chỉ đúng cho cơ học lượng tử bất tương đối, phép giải này cho nguyên tử hydro không phải là trọn vẹn đúng chuẩn. Phương trình Dirac của lí thuyết lượng tử tương đối cải tổ phép giải trên ( xem bên dưới ) .

Hệ quả của phương trình Schrödinger[sửa|sửa mã nguồn]

Phép giải của phương trình Schrödinger (phương trình sóng) cho nguyên tử hydro sử dụng tính chất lực tĩnh điện được sản xuất bởi hạt nhân là đẳng hướng (nó đối xứng trong không gian và chỉ phụ thuộc vào khoảng cách đến hạt nhân). Mặc dù những trạng thái dừng (orbital) không nhất thiết phải tự đẳng hướng, sự phụ thuộc của chúng vào các tọa độ cầu theo sau là hoàn toàn từ sự đẳng hướng của nguồn nằm dưới: những vector riêng của toán tử Hamilton (trạng thái năng lượng lượng tử) có thể được chọn như những vector riêng đồng thời của toán tử mô men động lượng.Điều này tương ứng với thực tế là mô men động lượng được bảo tồn trong orbital chuyển động của electron xung quanh hạt nhân. Vì vậy, trạng thái năng lượng lượng tử có thể được phân loại bởi hai số lượng tử mô men động lượng, ℓ và m (cả hai đều là số nguyên). Số lượng tử mô men động lượng ℓ = 0, 1, 2,… xác định tầm quan trọng của mô men động lượng. Số lượng tử từ m = −ℓ,…, +ℓ  xác định hình chiếu của mô men động lượng (chọn tùy ý) trên trục z.

Ngoài các biểu thức toán học cho mô men động lượng tổng và mô men động lượng chiếu của hàm sóng, một biểu thức cho đặc tính hàm sóng phụ thuộc bán kính phải được tìm thấy. Chỉ ở ngay đây mà các chi tiết của 1/r Coulomb có tiềm năng (dẫn đến đa thức Laguerre trong r). Điều này dẫn đến một số lượng tử thứ ba, số lượng tử chính n = 1, 2, 3,…. Số lượng tử chính hydro liên quan đến tổng năng lượng của nguyên tử.

Lưu ý rằng các giá trị lớn nhất của mô men động lượng bị giới hạn bởi số lượng tử chính: nó chỉ có thể lên tới n − 1, tức là ℓ = 0, 1,…, n − 1.

Do sự chuyển đổi mô men động lượng, các trạng thái của cùng một ℓ nhưng khác m có cùng năng lượng (điều này chịu trách nhiệm cho tất cả các vấn đề với đối xứng quay). Ngoài ra, với nguyên tử hydro, trạng thái cùng n, nhưng khác ℓ cũng thoái hóa (tức là chúng cùng một năng lượng). Tuy nhiên, điều này là một đặc tính riêng biệt của hydro và không còn đúng cho các nguyên tử phức tạp hơn có một tiềm năng (hiệu quả) khác nhau từ dạng 1/r (do sự hiện diện của các hạt nhân tiềm năng).

Thêm vào sự hiện diện của spin của electron thêm vào một số lượng tử cuối cùng, các hình chiếu của mô men động lượng của electron dọc trục z, trong đó có thể có hai giá trị. Vì vậy, bất kỳ trạng thái lượng tử nào của electron trong nguyên tử hydro được mô tả đầy đủ bằng bốn số lượng tử. Theo các quy tắc thông thường của cơ học lượng tử, thực trạng của electron có thể là bất kì chồng chấp lượng tử của những trạng thái này. Điều này giải thích tại sao sự lựa chọn của trục z cho các hướng lượng tử hóa của vector mô men động lượng là phi vật chất: một orbital của  ℓ và m‘ lấy cho một trục z‘ khác luôn có thể được biểu thị như là một chồng chất lượng tử phù hợp các trạng thái của các m khác nhau (nhưng cùng l), mà đã được lấy cho trục z.

Khái lược toán học của những trạng thái lượng tử của nguyên tử hydro[sửa|sửa mã nguồn]

Năm 1928, Paul Dirac tìm thấy một phương trình trọn vẹn thích hợp với thuyết tương đối hẹp, và ( như một hệ quả ) đã làm hàm sóng thành một ” spinor Dirac ” 4 phần gồm có phần spin ” lên ” và ” xuống “, với spin dương và âm, ( hay là vật chất và phản vật chất ). Cách giải phương trình này cho những tác dụng đúng chuẩn hơn phép giải Schrödinger .

Mức nguồn năng lượng[sửa|sửa mã nguồn]

Mức nguồn năng lượng của hydro, gồm có cả cấu trúc tinh xảo ( ngoại trừ hiệu ứng Lamb và cấu trúc siêu tinh xảo ), được đưa ra bởi những biểu thức hằng số cấu trúc tinh xảo : [ 10 ]

E j n = − m e c 2 [ 1 − ( 1 + [ α n − j − 1 2 + ( j + 1 2 ) 2 − α 2 ] 2 ) − 1 / 2 ] ≈ − m e c 2 α 2 2 n 2 [ 1 + α 2 n 2 ( n j + 1 2 − 3 4 ) ], { \ displaystyle { \ begin { array } { rl } E_ { j \, n } và = – m_ { \ text { e } } c ^ { 2 } \ left [ 1 – \ left ( 1 + \ left [ { \ dfrac { \ alpha } { n-j – { \ frac { 1 } { 2 } } + { \ sqrt { \ left ( j + { \ frac { 1 } { 2 } } \ right ) ^ { 2 } – \ alpha ^ { 2 } } } } } \ right ] ^ { 2 } \ right ) ^ { – 1/2 } \ right ] \ \ và \ approx – { \ dfrac { m_ { \ text { e } } c ^ { 2 } \ alpha ^ { 2 } } { 2 n ^ { 2 } } } \ left [ 1 + { \ dfrac { \ alpha ^ { 2 } } { n ^ { 2 } } } \ left ( { \ dfrac { n } { j + { \ frac { 1 } { 2 } } } } – { \ dfrac { 3 } { 4 } } \ right ) \ right ], \ end { array } } }{\displaystyle {\begin{array}{rl}E_{j\,n}&=-m_{\text{e}}c^{2}\left[1-\left(1+\left[{\dfrac {\alpha }{n-j-{\frac {1}{2}}+{\sqrt {\left(j+{\frac {1}{2}}\right)^{2}-\alpha ^{2}}}}}\right]^{2}\right)^{-1/2}\right]\\&\approx -{\dfrac {m_{\text{e}}c^{2}\alpha ^{2}}{2n^{2}}}\left[1+{\dfrac {\alpha ^{2}}{n^{2}}}\left({\dfrac {n}{j+{\frac {1}{2}}}}-{\dfrac {3}{4}}\right)\right],\end{array}}}

với α la hằng số cấu trúc tinh tế và j là số lượng tử “tổng mô men động lượng”, là bằng |ℓ ± 1/2| tùy thuộc vào sự hướng của các spin electron. Công thức này đại diện cho một điều chỉnh nhỏ đến năng lượng đạt được bởi lí thuyết Bohr và Schrödinger được đưa ra phía trên. Các yếu tố trong ngoặc vuông cuối cùng gần như là một; thuật ngữ phát sinh từ những hiệu ứng tương đối (xem chi tiết #Tính chất vượt ra ngoài phép giải Schrödinger). Rất đáng chú ý là biểu thức này lần đầu tiên được phát hiện bởi A. Sommerfeld vào năm 1916, dựa trên phiên bản tương đối của lí thuyết Bohr cũ. Tuy nhiên, ông đã dùng những kí hiệu khác cho các số lượng tử.

Mô phỏng orbital electron hydro[sửa|sửa mã nguồn]

Mật độ xác suất qua mặt phẳng xz cho electron ở các số lượng tử khác nhau (ℓ, dãy trên đầu, n, dãy xuống dưới; m = 0)

Bên phải ảnh cho thấy những orbital nguyên tử hydro đầu tiên (vector riêng năng lượng). Đây là mặt cắt của biên độ xác suất đã được tô màu (đen đại diện cho mật độ không và màu trắng đại diện cho mật độ cao nhất). Số lượng tử mô men động lượng (orbital) ℓ được biểu thị trong mỗi cột, bằng cách sử dụng mã quang phổ thông thường (s có nghĩa là ℓ = 0, p có nghĩa là ℓ = 1, d có nghĩa là ℓ = 2). Số lượng tử chính n (= 1, 2, 3,…) nằm ở phía bên phải mỗi hàng. Trong tất cả các ảnh, số lượng tử từ m đã được đặt về 0, và mặt phẳng cắt ngang là mặt phẳng xz (z là trục đứng). Biên độ xác suất trong ba chiều không gian thu được bằng cách xoay quanh trục z.

“Trạng thái cơ bản”, hay nói cách khác là trạng thái năng lượng thấp nhất, trong đó electron thường được tìm là trạng thái đầu tiên, trạng thái 1s (mức lượng tử chính n = 1, ℓ = 0).

Đường thẳng đen xảy ra trong mỗi orbital, nhưng orbital tiên phong : đây là những giao điểm của hàm sóng, tức là nơi mà có biên độ Xác Suất bằng không. ( Chính xác hơn là, những giao điểm là những hàm điều hòa cầu Open như là một hiệu quả của việc giải phương trình Schrödinger ở tọa độ cực. )Các số lượng tử xác lập cách sắp xếp của những giao điểm. [ 11 ] Chúng là :

  • n − 1 { \ displaystyle n-1 }{\displaystyle n-1}
  • l { \ displaystyle l }{\displaystyle l}
    • m { \ displaystyle m }m{ \ displaystyle }{\displaystyle }(Hình trên không hiển thị những giao điểm này vì chúng cắt ngang qua mặt phẳng xz.)
    • l − m { \ displaystyle l-m }{\displaystyle l-m}{ \ displaystyle }
  • n − l − 1 { \ displaystyle n-l-1 }{\displaystyle n-l-1}

Tính chất vượt ra ngoài phép giải Schrödinger[sửa|sửa mã nguồn]

Có một vài hiệu ứng quan trọng bị bỏ lỡ trong phương trình Schrödinger, và điều đó là lí do một số ít vạch quang phổ ngoài thực tiễn bị lệch đi một chút ít so với những gì đã Dự kiến :

  • Mặc dù tốc độ của electron trong hydro chỉ bằng 1/137 tốc độ ánh sáng, nhiều thí nghiệm hiện đại với độ chính xác rất cao yêu cầu một lí thuyết hoàn chỉnh giải thích sự xử lí tương đối của vấn đề. Một kết quả xử lí tương đối cho ra một mô men tăng khoảng 1 phần trong 37,000 cho electron. Vì bước sóng của electron được xác định theo mô men của nó, những orbital có chứa electron tốc độ cao cho thấy sự co rút do bước sóng nhỏ hơn.
  • Thậm chí khi không có từ trường bên ngoài, trong các khung quán tính của electron đang chuyển động, trường điện từ của hạt nhân cũng có một phần tử từ trường. Spin của electron có liên quan đến mô men lưỡng cực từ, thứ mà tương tác với từ trường này. Hiệu ứng này cũng đã được giải thích bởi thuyết tương đối hẹp, và nó dẫn đến cái gọi được là spin-quỹ đạo cặp, tức là một sự tương tác giữa orbital chuyển động của electron xung quanh hạt nhân, và spin của nó.

Cả hai năng tính chất này (và nhiều hơn nữa) được tích hợp vào trong phương trình Dirac tương đối với các dự đoán đến gần hơn với thí nghiệm. Một lần nữa, phương trình Dirac có thể được giải tích phân trong những trường hợp đặc biệt của hệ thống hai vật, như nguyên tử hydro. Các kết quả trạng thái lượng tử bây giờ phải được phân loại bởi các số lượng tử mô men động lượng tổng j (phát sinh qua sự cặp giữa spin electron và toán tử mô men động lượng). Trạng thái có cùng j và cùng n vẫn thoái hóa. Vì vậy, phép giải tích phân trực tiếp của phương trình Dirac dự đoán mức Hydro 2S(1/2) và 2(1/2) có chính xác cùng một năng lượng, thứ mâu thuẫn với các quan sát của thí nghiệm Lamb-Retherford.

  • Luôn có các dao động chân không của trường điện từ dựa theo cơ học lượng tử. Do những sự thoái hóa dao động như vậy giữa trạng thái của cùng j nhưng khác l được đẩy lên, cho chúng một chút năng lượng khác nhau. Điều này đã được chứng minh trong thí nghiệm Lamb-Rutherford nổi tiếng và là thời điểm khởi đầu cho sự phát triển của những lí thuyết về điện động lực học lượng tử (thứ mà có thể đối phó với những dao động chân không và sử dụng sơ đồ Feynman xấp xỉ bằng lí thuyết nhiễu loạn). Hiệu ứng này ngày nay được gọi là hiệu ứng Lamb.

Với những tăng trưởng này, đó là điều tất yếu với phép giải của phương trình Dirac cho nguyên tử hydro hoàn toàn có thể được hoạt động giải trí vô cùng đúng chuẩn như vậy, nên khi bất kể rơi lệch nào được quan sát phải được nhận định và đánh giá một cách trang nghiêm như thể một tín hiệu của sự thất bại của lí thuyết .

Những lí thuyết khác cho lí thuyết Schrödinger[sửa|sửa mã nguồn]

Trong ngôn từ của cơ học ma trận Heisenberg, những nguyên tử hydro đã được xử lý tiên phong bởi Wolfgang Pauli bằng cách sử dụng một đối xứng quay trong khoảng trống bốn chiều [ đối xứng O ( 4 ) ] được tạo ra bởi mô men động lượng và vector Laplace-Runge-Lenz. Bằng cách lan rộng ra nhóm đối xứng O ( 4 ) đến nhóm động lực O ( 4,2 ), hàng loạt phổ và tổng thể những pha chuyển được nhúng trong một đại diện thay mặt nhóm bất khả giảm duy nhất. [ 12 ]Vào năm 1979, nguyên tử hydro ( bất tương đối ) đã được xử lý lần tiên phong trong công thức tích phân của cơ học lượng tử của Richard Feynman. [ 12 ] [ 12 ] Thành quả này lan rộng ra rất nhiều khoanh vùng phạm vi vận dụng của giải pháp của Feynman .

Liên kết ngoài[sửa|

sửa mã nguồn]

Sửa Tủ Lạnh

Trung Tâm Bảo Hành

Alternate Text Gọi ngay